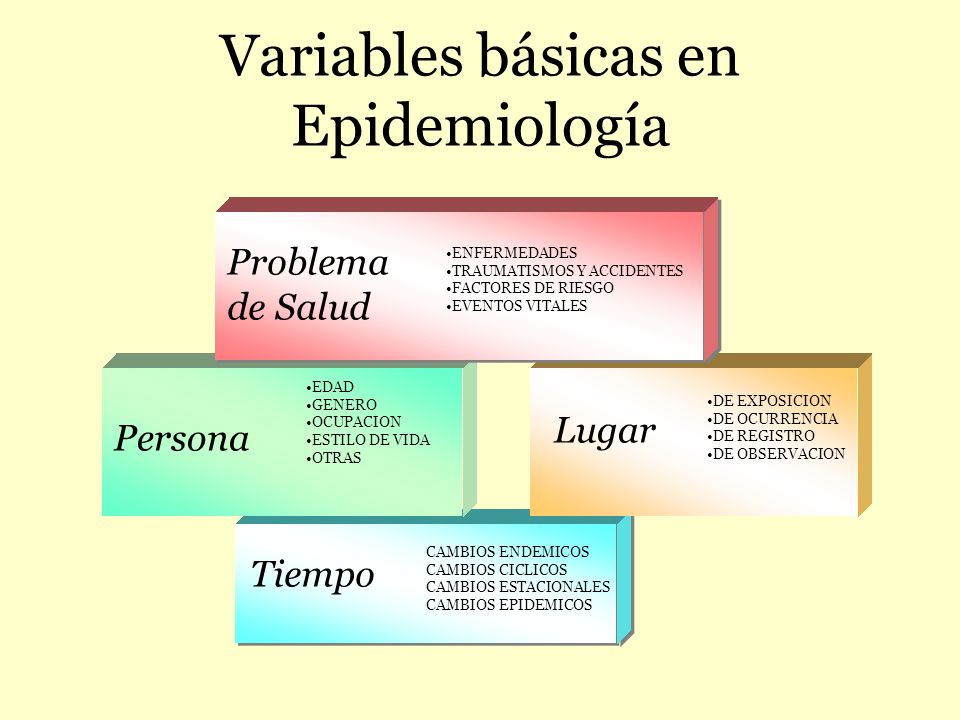
Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan a otro punto llamado centro. Si el plano es perpendicular a dicho eje produce una circunferencia. El eje forma con el plano 90º = β

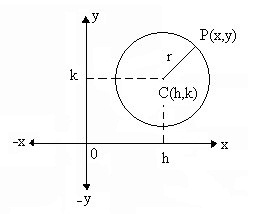

Esas ecuaciones corresponden a las ecuaciones canónicas, la primera con centro en el origen del plano cartesiano y la segunda cuando el centro esta en cualquier parte del plano, inclusive en el centro, simplemente en el centro h = 0 y k = 0, la otra presentación es la ecuación general de segundo grado:
Ax^2+By^2+Dx+Ey+F=0
Se considera que la ecuación se considera una circunferencia cuando A = B; ambas positivas > 0 (+) o ambas negativas < 0 (-).
EJEMPLO 1
El siguiente vídeo nos ilustra paso a paso como hallar las ecuaciones canónica y general de la CIRCUNFERENCIA conociendo el centro y el radio (duración 7'10").
EJEMPLO 2
El siguiente vídeo nos ilustra paso a paso como encontrar el centro y radio de la CIRCUNFERENCIA conociendo la ecuación general de segundo grado. Se resuelve por dos métodos distintos, en la primera lo hace por formula (es muy corto el proceso) y el segundo haciendo la completación del cuadrado. No se realiza la gráfica (duración 11'10").
EJEMPLO 3
El siguiente vídeo nos ilustra paso a paso como elaborar la gráfica de la CIRCUNFERENCIA conociendo el centro y el radio; graficar una CIRCUNFERENCIA cualquiera que sea su presentación se reduce a conseguir el centro y el radio (duración 6'12").
Te sugiero complementar la información en la unidad didáctica de Geometría Analítica, Cónicas y Probabilidad.